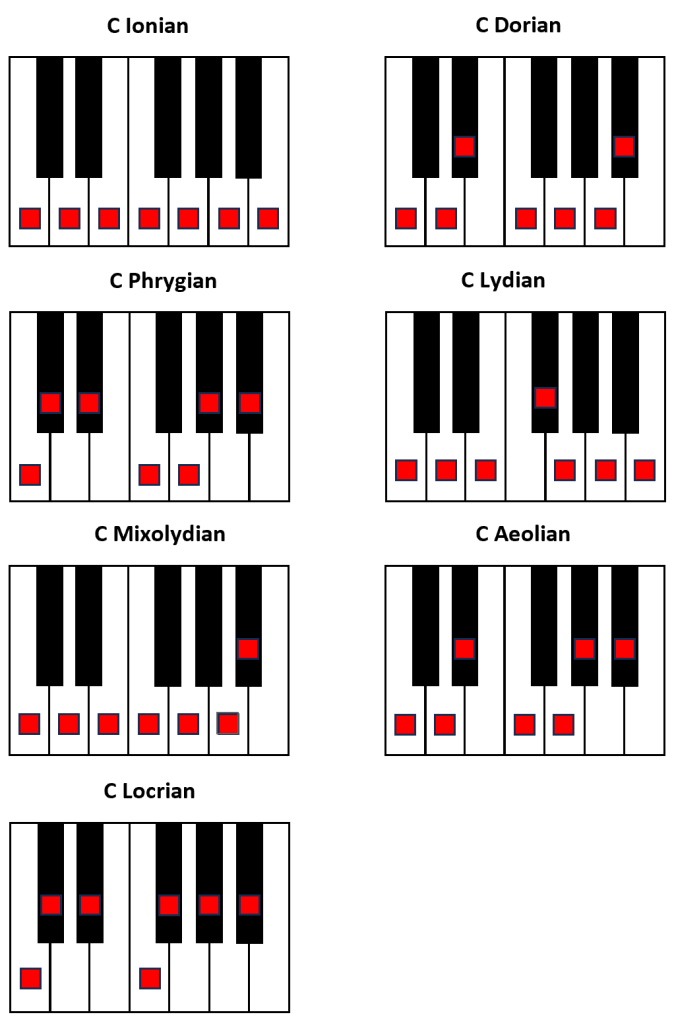
In this essay, I will explore a mathematical property of musical modes that may not have direct practical use for musicians or composers, but could intrigue mathematically inclined readers: the notion of symmetry. Let’s consider the C Ionian mode—also known as the C major scale. When played in ascending order, we can ask: what scale would produce the same sequence of intervals if played in descending order? Put differently, what is the symmetric scale—one that mirrors the original intervals in reverse? This is precisely what emerges when we apply the interval pattern in reverse, mode by mode. In the table below, intervals are measured in semitones (“s”).
| Mode | Intervals | Reversed Intervals | Mode of Reversed Intervals |
|---|---|---|---|
| Ionian | 2s 2s 1s 2s 2s 2s 1s | 1s 2s 2s 2s 1s 2s 2s | Lydian |
| Dorian | 2s 1s 2s 2s 2s 1s 2s | 2s 1s 2s 2s 2s 1s 2s | Phrygian |
| Phrygian | 1s 2s 2s 2s 1s 2s 2s | 2s 2s 1s 2s 2s 2s 1s | Dorian |
| Lydian | 2s 2s 2s 1s 2s 2s 1s | 1s 2s 2s 1s 2s 2s 2s | Ionian |
| Mixolydian | 2s 2s 1s 2s 2s 1s 2s | 2s 1s 2s 2s 1s 2s 2s | Locrian |
| Aeolian | 2s 1s 2s 2s 1s 2s 2s | 2s 2s 1s 2s 2s 1s 2s | Aeolian |
| Locrian | 1s 2s 2s 1s 2s 2s 2s | 2s 2s 2s 1s 2s 2s 1s | Mixolydian |

Let us now delve a little deeper in this topic. The question I would like to answer is whether the mode-symmetry tables represented above abide by a mathematical equation. In the following page, we will see that the answer is affirmative. For convenience’s sake, we will need to represent the seven modes with their respective ordinal.
| Ordinal | Mode |
|---|---|
| 1 | Ionian |
| 2 | Dorian |
| 3 | Phrygian |
| 4 | Lydian |
| 5 | Mixolydian |
| 6 | Aeolian |
| 7 | Locrian |
Proposition
Let us consider any given mode out of the list above. We will refer to it as mode(i), where i is its ordinal. The symmetric mode of mode(i) is mode(j), where i and j satisfy the following equation:
(i + j) mod 7 = 4
The proof will proceed by case:
- Ionian
As we have seen above, the symmetric mode of Ionian is Phrygian. Ionian has ordinal 1, whereas Phrygian has 3. Hence: (1 + 3) mod 7 = 4 mod 7 = 4
- Dorian
As we have seen above, the symmetric mode of Dorian is Dorian itself. Dorian has ordinal 2. Hence: (2 + 2) mod 7 = 4 mod 7 = 4
- Phrygian
Since symmetry is, by definition, a symmetric relation, the fact that Ionian is the symmetric mode of Phrygian implies that Phrygian is the symmetric mode of Ionian.
- Lydian
As we have seen above, the symmetric mode of Lydian is Locrian. Lydian has ordinal 4, whereas Locrian has 7. Hence: (4 + 7) mod 7 = 11 mod 7 = 4
- Mixolydian
As we have seen above, the symmetric mode of Mixolydian is Aeolian. Mixolydian has ordinal 5, whereas Aeolian has 6. Hence: (5 + 6) mod 7 = 11 mod 7 = 4
- Aeolian
Since symmetry is, by definition, a symmetric relation, the fact that Mixolydian is the symmetric mode of Aeolian implies that Aeolian is the symmetric mode of Mixolydian.
- Locrian
Since symmetry is, by definition, a symmetric relation, the fact that Lydian is the symmetric mode of Locrian implies that Locrian is the symmetric mode of Lydian.
♦