A very good introduction to Cellular Automata is available in Wikipedia. For convenience’s sake we will give a brief description to the extent required to understand this article.
Definition – Cellular Automaton
A Cellular Automaton (CA) is a model of computation based on a grid of cells, each of which can be in a finite number of states. CA evolve at discrete times, starting from their initial state at time t0, based on a function which remains the same over the life of the CA and is applied to all its cells.
♦
Definition – Neighbours of a cell
neighbors: Cell -> Vector(Cell) is a total function which for every cell c ∈ CA.cells returns its neighbourhood.
Intuitively, this represents a notion of adjacency.
♦
Definition – states
States = { live, dead }
♦
Definition: Transition function
The transition function f: (Cell, Vector(Cell)) -> State is a total function on CA.cells such that:
∀c: Cell, c.statet+1 = f(c.statet, neighbours(c).statet)
where the expression neighbours(c).statet denotes the state at time t of each cell returned by neighbours(c)
♦
Remark
It is important to note that the new state at time t+1 of all the cells in a CA is computed based on the states at time t. In other words, partial updates of a CA will not affect the determination of other cell states for the same update cycle.
Remark
A grid in a CA can have any finite number of dimensions. Two-dimensional grids are popular because their status is easy to display graphically.
Definition
- alive_neighbourst(c) is the set of cells in neighbours(c) which are in state live at time t
- dead_neighbourst(c) is the set of cells in neighbours(c) which are in state dead at time t
♦
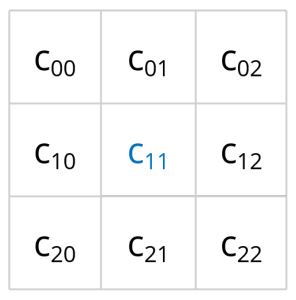
Conway’s game of life
A popular example of cellular automaton is Conway’s game of life. In this case cells can assume the two states live or dead and are part of a two-dimensional grid. Every cell has therefore eight neighbours:
neighbours(c11) = { c00, c01, c02, c10, c12, c20, c21, c22 }
The transition function of Conway’s game of life can be summarised as follows:
- ∀c: Cell, such that c.statet = live ∧ 2 <= #alive_neighbourst(c) <= 3, we have c.statet+1 = live (“the cell survives”)
- ∀c: Cell, such that c.statet = dead∧ #alive_neighbourst(c) = 3, we have c.statet+1 = live (“the cell becomes alive”)
- For any other cell c for which neither 1 nor 2 above apply, we have c.statet+1 = dead (“if c is alive it dies, otherwise it stay dead”)
♦
In the general definition of Cellular Automata nothing says that cells must be placed in a grid. In the remainder of this article we will write a Scala programme capable of computing the states of Cellular Automata based on binary trees. This programming challenge is described on website hackerrank.com: The Tree of Life Problem.
Cellular Automata on Binary Trees
In this type of Cellular Automata cells live in a binary tree. The following picture exemplifies the concept:

Cell c0.0.0 is highlighted because I will use it to illustrate concepts such as the neighbours() function and the transition function.
Neighbours of a cell in a binary tree
The following picture shows what are the neighbours of cell c0.0.0 in the binary tree:

Definition – function neighbours() on a binary tree
The neighbours of a cell in a binary tree are:
- its parent cell
- its left child cell
- its right child cell
If any of they neighbours listed above should not exist, a fictitious default cell is taken, whose state is false.
♦
Definition – transition function f() on a binary tree
The transition function f: States4 -> State is a total function defined as follows:
∀c: Cell, c.statet+1 = f(c.statet, c.parent.statet, c.left-child.statet, c.right-child.statet)
♦
Remark
c.parent, c.left-child, and c.right-child always return a cell, even if it is does not exist in the tree. Based on the definition above, in these cases a default cell with state false will be returned.
How can the transition function f be represented
A convenient way to model the transition function is through a table:

click on the image to enlarge it
Proposition – the number of possible transition functions for a cellular automaton in a binary tree is 2^16 = 65’536
This is obviously true in that there are 2^4=16 possible combinations of states for a cell and its neighbours, and for each such combination the transition function can assume one out of two values (live/dead).
♦
Remark
In the table above, the mapping of columns to a cell and its neighbours determines an ordering. This choice corresponds with the specification of the sorting criterion defined for our programming exercise The Tree of Life Problem
Syntax for serialised cell binary trees
We now need to define the syntax in order to be able to read serialised binary tree from the command line. The grammar of a binary tree is simple and can be given like this using the Backus Naur form:
<node> ::= 'X' | '.'
<btree> ::= <node> | '('<btree>' '<node>' '<btree>')'
where:
- ‘X’ signifies live, whereas ‘.’ signifies dead.
- given a tree expression of the form “(expr1 expr2 expr3 )”, expr2 is the node, expr1 is its left child, and expr3 is its right child.
♦
Examples
- X
- .
- (X . .)
- ((X . .) X (X . X))
- ((X . .) X (X . X)) X ((. X X) . (. X .))

♦
Defining the transition function
Now that we know how to represent a CA binary tree, we need to define a suitable format for a transition function. All we need to consider is that a transition function is an ordered sequence of states of length 16. Given that states are live or dead, we can easily represent them as a 1 or a 0, respectively. Then, a convenient representation of a transition function is an integer n such that 0 <= n <= 65’535.
The Scala primitive type for an unsigned 16-bits integer is Char.
♦
Reading the state of a particular node in a binary tree
Paths to a cell will be expressed relative to the root node. Every time the tree is traversed through the left sub-tree we will denote the move using character ‘<‘; when the right sub-tree is traversed we will use a ‘>’. Traversal paths will be delimited by square brackets. Examples:
- []
- [<]
- [><<><>>>]
- [<><]
where case 1 is the empty path and case 4 is illustrated by the following picture:

This syntax is arbitrary. One could as well write the paths above using characters ‘L’ and ‘R’ for left or right, respectively. We will use this syntax as specified by The Tree of Life Problem.
Historisation of past states
In order to solve the programming challenge we will need to historise the changes we apply to the tree every time we evolve it to the next generation by running the transition function as many times as requested. The number of times is expressed with a signed integer. The position in the history may be before the last element because, as we will see, time can go in the past.
Let us assume that:
- The history has n generations (n trees whose states have been determined through subsequent applications of the transition function).
- The current position in the history is m, with 0<= m <= n – 1 (history is 0-based)
If we are asked to apply the transition function t times, this is what our program must do:
- if t >= 0 and m+t < n then m := t+m (move the current position ahead t times)
- else if t >= 0 and m+t >= n then {
- m := n-1 (move current position in history to the last one)
- for i=1 to m + t – n + 1 {
- apply transition function f to the tree at position m
- add the tree resulting from point above to the history
- move current position to the last one (tree just generated)
- }
- } else if t < 0 and m+t >= 0 {
- m := m + t (go back in history t times)
- } else ERROR
Examples
(click on the image above to enlarge it)
Input syntax
Input will be passed to the program through the command line.
- The first line will be an integer expressing the transition function.
- The second line will be a serialised cellular automaton binary tree.
- The third line is an integer expressing the number of queries.
- The subsequent lines will be as many as the number of queries as per the above.
- Each query has the following syntax: <integer> <path expression>
The program must interpret the integer in the queries as explained above (Historisation of past states), read the state of the node denoted by the root-based traversal path in the same query, and print it to the standard output before processing the next query.
Example
23749 ((X . .) X (X . X)) X ((. X X) . (. X .)) 7 3 [] 2 [><] -1 [<>] -1 [<><] 12 [<<<] -2 [>><] 1 [>>>]
♦
Assumptions
In this exercise we can safely assume that the traversal paths will be valid and that the history will not be explored before the start of time (generation zero).
♦
We now have the conceptual framework required to start with the implementation. Let’s code!!!
Defining a node in the binary tree
sealed trait Status
object On extends Status
object Off extends Status
case class Node(s: Status) {
override def toString = s match {
case On => "X"
case Off => "."
}
}
object Node {
val on = Node(On)
val off = Node(Off)
}
At the moment of writing, website hackerrank.com supports Scala 2, not 3. This is why I have chosen a sealed trait with two objects instead of a simple enumeration to represent the state (Status in the code). In this way we have only two objects to represent the states. Object Status.On represents state live, whereas object Status.Off represents dead.
Class Node is trivial in that only has an attribute which is the state. Companion object Node returns two objects Node.on and Node.off with the obvious meaning. Please note that using objects like this guarantees that the number of instances in memory is strictly under control. If you do not know what is a companion object, please refer to http://www.scala-lang.org
Method toString() is overridden so that the string representation of the states matches the syntax requirements for this exercise.
Defining a cell
The definition of a node above may give the impression that there is no need to define yet another one for a cell. However, for reasons which will be clearer later, I will define a cell as a class with four attributes: a parent node, its own node, its left child node, and its right child node.
case class Cell(parent: Node, self: Node, left: Node, right: Node)
This definition will make the application of the transition function (the rule) simpler.
Defining a binary tree
Now that we have a node, we can easily define a binary tree.
case class BTree(n: Node, left:Option[BTree], right: Option[BTree])
A binary tree is defined as a structure formed by a node and two optional child trees. But before we delve deeper into the implementation of the BTree, we need to introduce the notion of a Rule.
Defining the rules
case class Rule(r: Char)
A rule is a Char. At this point you may be wondering why. The reason is that, as we have seen above, rules are sequences of 16 values (on/off, or live/dead, etc.). Char in Scala is an unsigned integer of exactly 16 bits. Therefore, it is an extremely compact way to encode a transition function (or a rule, using hackerrank’s terminology).
We can continue with the implementation of rules, by preparing useful data structures by means of the Rule companion object:
object Rule {
val nodeTypes = Vector(Node.off, Node.on)
val sortedCells = nodeTypes.flatMap(n0 => nodeTypes.flatMap(n1 => nodeTypes.flatMap(n2 => nodeTypes.map(n3 => Cell(n0, n2, n1, n3)))))
val ruleIndex: Map[Cell, Int] = sortedCells.indices.map(i => (sortedCells(i) -> i)).toMap
val bits: Vector[Char] = (1 to 16).map(n => pow(2, n-1).toChar).toVector
}
The above needs some explaining.
- nodeTypes is an ordered sequence of node types modelled as a Vector (please note that no new instance of Node has been created, we are using the singletons defined above).
- sortedCells is an ordered sequence of all the possible Cells created by generating all the combinations of off and on, and creating a Cell for each of them paying attention to the sort order defined by the author of this exercise who specifies that:
- The state of the parent node comes first
- The state of the left child node comes second
- The state of the node whose new value we are computing comes third
- The state of the right child node comes fourth
- ruleIndex is a map which for every possible Cell returns the index of the value in the rule (please refer to the explanation above on how the rules are modelled).
- bits is a Vector which for every bit index in the rule gives the corresponding binary representation of the on flag. For example, at position 0 it gives 0000000000000001. At position 1 it gives 000000000000010 and so on until position 15 where we have 1000000000000000.
We will better understand the use of the above when we will see how a rule is applied to a binary tree to evolve it to the next generation.
Applying a rule to a cell
case class Rule(r: Char) {
def applyTo(c: Cell): Node = if ((bits(ruleIndex.getOrElse(c, -1)) & r) > 0) Node.on else Node.off
}
Let us assume that we are now applying a rule to a specific cell. Thanks to the plumbing above the implementation is trivial. First we look for the index in the rule where the new value of the cell is specified. In order to get this index we just have to use our map ruleIndex which contains all the possible cells (key) and their indexes (value). Once we know this index, we get the binary representation of an on flag (a 1) and we compute the logical AND of this flag with the value specified in the rule. If the result of this logical AND is different from 0 than the new state is on, otherwise it is off. This is illustrated by the following picture:

click on picture to enlarge
Remark
You will have noticed that I have used method getOrElse() and may be wondering why, given that by construction, I know that I will find my cell (given that ruleIndex contains all the possible cells). The reason is that the compiler does not know that the operation is safe because a get() on a map in general can fail. Therefore I return -1 in case the cell is not found (which cannot happen).
Applying a rule to the entire tree
case class BTree(n: Node, left:Option[BTree], right: Option[BTree]) {
def applyRule(r: Rule, parent: Node = Node.off): BTree = {
def nextCell(o: Option[BTree]) = o match {
case Some(t) => t.n
case None => Node.off
}
def subTree(o: Option[BTree]) = o match {
case Some(t) => Some(t.applyRule(r, n))
case None => None
}
BTree(r.applyTo(Cell(parent, n, nextCell(left), nextCell(right))), subTree(left), subTree(right))
}
Method BTree.applyRule() above generates the next generation tree one node at a time by traversing itself recursively and computing the new state of each and every node.
Please note that the value of parameter parent is set to Node.off by default. This is useful because we start from the root of the tree which, by definition, does not have a parent node. You may wonder why than assign Node.off? The reason is that this is the desired behaviour specified by the author of this programming exercise. Let us now focus on the recursion. First, we need to identify the base case. Then, we must identify the recursion step. We will proceed using structural recursion. The base step is of course the node. We already know how to apply a rule to a node, we have seen it above. What we still need to add is that when a node does not have its parent (root) or one or two child nodes, we will assign default node Node.off. Again, this is the desired behaviour as per specs of this exercise. See The Tree of Life Pro for details (including discussion forums). The step is defined as follows: the new generation of:
BTree(n: Node, left: Option[BTree], right: Option[BTree])
is a new BTree having:
- its node transformed by rule r: r.applyTo(Cell(parent, n, nextCell(left), nextCell(right)))
- its sub trees t having node n recursively transformed applying rule r: t.applyRule(r, n)
Remarks
- we use method def nextCell(o: Option[BTree]) to find the node of sub-trees, so that in case there is none, we can assign default value Node.off
- we use method def subTree(o: Option[BTree]) to transform a sub-tree, because in case there is none, we just return None instead of starting a new recursive call
If you do not know what is Option[T] in Scala and the meaning of Some(), None, please refer to http://www.scala-lang.org
Now that we know how to transform a binary tree, we are ready to write a method which reads the state of any node given a correct root-based path expression.
Reading the state of a node
case class BTree(n: Node, left:Option[BTree], right: Option[BTree]) {
@tailrec
final def readNode(path: List[Char]): Node = path match {
case Nil => n
case h :: pp => val next = h match {
case '<' => left
case '>' => right
case _ => None
}
next match {
case Some(t) => t.readNode(pp)
case None => n
}
}
}
Remark
We have seen above that the syntax of a path used in the queries is an arbitrary sequence of ‘<‘ and ‘>’ symbols enclosed by ‘[‘ and ‘]’. Method readNode() expects the path to be without any enclosing square brackets, only a sequence of ‘<‘ and ‘>’.
Method readNode() uses the character at the current position in the path to determine if the tree traversal must continue to the left or to the right, and proceeds recursively passing the path without the character just processed to the selected child tree.
Error management
- if the path is empty than return the current node
- if there is an unexpected character in the path (neither ‘<‘ nor ‘>’), than return the current node
Annotation @tailrec
You may have noticed that method readNode() has annotation @tailrec. If you do not know what it means, it is a property denoting recursive algorithms satisfying stricter conditions which allow the compiler to generate very efficient code, which makes the runtime performance of this type of recursion comparable to the performance of traditional loop control structures. In other words, you will not have to worry about the recursion running too deep and the method running out of stack. You may find better definitions of a tail recursive algorithm but, for the purposes of this article, I will just say that the intuitive notion entails ending the method with the recursive call. The recursive call is the very last thing which the method does.
Writing the parser
Above we said that the input has a syntax exemplified by this excerpt:
23749 ((X . .) X (X . X)) X ((. X X) . (. X .)) 7 3 [] 2 [><] -1 [<>] -1 [<><] 12 [<<<] -2 [>><] 1 [>>>]
Reading the rule is trivial:
val rule = Rule(readInt.toChar)
Reading the tree and the queries may be a little bit more involved.
Parsing the tree
@tailrec
def getTreeExpr(s: String, expr: String = "", depth: Int=0): (Option[String], String) = {
if (s.isEmpty) (None, expr + s) else s(0) match {
case '(' => getTreeExpr(s.substring(1), expr + s(0), depth + 1)
case ')' => if (depth == 1) (Some((expr + s(0)).trim), s.substring(1))
else getTreeExpr(s.substring(1), expr + s(0), depth - 1)
case c => if (Set(' ', 'X', '.').contains(c))
getTreeExpr(s.substring(1), expr + s(0), depth)
else (None, expr + s)
}
}
Method getTreeExpr() scans an input string one character at a time checking that only characters defined in the grammar of a tree expression are used (see section above) and that the brackets are balanced.
If a valid tree expression is recognised, it is returned as Some()[String], otherwise None is returned. The remaining part of the input string is also returned along with the recognised tree expression (or None in case of errors).
Please, note that the implementation of this method is also @tailrec.
Building the BTree from a valid tree expression
@tailrec
def parseNode(s: String): (Option[Node], String) =
if (s.isEmpty) (None, s) else s(0) match {
case 'X' => (Some(Node.on), s.substring(1))
case '.' => (Some(Node.off), s.substring(1))
case ' ' => parseNode(s.substring(1))
case _ => (None, s)
}
def parseTree(s: String): (Option[BTree], String) =
if (s.isEmpty) (None, s) else parseNode(s) match {
case (Some(n), rem) => (Some(BTree(n, None, None)), rem)
case (None, _) => getTreeExpr(s) match {
case (None, rem) => (None, rem)
case (Some(exp), rem) => (BTree(exp), rem)
}
}
We will start with method readNode().
- If symbol ‘X’ is encountered than Some(Node.on) is returned
- If symbol ‘.’ is encountered than Some(Node.off) is returned
- If symbol ‘ ‘ (a blank) is encountered than move on to the next char in the string
- otherwise return None
Whatever the result of the scan, this method returns the remaining part of the input string.
Method parseTree()
- if the input string is empty, return None
- if the tree expression denotes a node n, return a BTree with node n and None as left and right sub-trees (leaf node)
- if the tree expression is not a valid node, parse the input to check if it is a valid a tree expression
- if not, return None and the input string
- otherwise build a tree based on the valid tree expression using method def apply(s:String): Option[BTree]
Method def apply(s:String): Option[BTree]
object BTree {
def apply(s:String): Option[BTree] =
if (s.length < 7) parseNode(s) match {
case (Some(n), _) => Some(BTree(n, None, None))
case _ => None
} else (s(0), s(s.length - 1)) match {
case ('(', ')') =>
val (left, lRem) = parseTree(s.substring(1, s.length - 1))
val (node, nRem) = parseNode(lRem)
val (right, rRem) = parseTree(nRem)
(node, left, right) match {
case (Some(n), Some(l), Some(r)) => Some(BTree(n, Some(l), Some(r)))
case _ => None
}
case _ => None
}
}
Before explaining method apply() it is worth noting that it uses method parseTree() which, as we have seen above, uses method apply(). This situation is called mutual recursion which for a functional programmer is the place “where eagles dare”.
Method apply() uses convenience methods parseNode() and parseTree() to deconstruct a serialised binary tree. From the grammar introduced above we know that a tree is represented as a triplet where the first part is the optional left child tree, the second one is the current node, and the last one is the optional right tree. In order to determine whether the input string must be parsed as a plain node or a binary tree, this method uses a cheap trick: checks the length. This works because we know that the simplest tree is formed by all nodes and has a form similar to “(X . X)” which are seven characters: left bracket, node symbol, blank, node symbol, right bracket. There may be more elegant ways to implement this part, but this works pretty well and is efficient so, for the purposes of this exercise, I will not try to do any better. But, of course, you can!
The apply() method proceeds with structural recursion: if a proper tree expression is recognised, its left and right sub-trees are recursively inspected, until the entire expression is processed, or an error is encountered.
We are now ready for the implementation of the parser for the queries.
Parsing the queries
We have seen above that queries have syntax exemplified by these expressions:
3 [] 2 [><] -1 [<>] -1 [<><] 12 [<<<] -2 [>><] 1 [>>>]
Parsing the first part is trivial: it is a signed integer. More interesting is parsing the second part. Here, I will use a regular expression.
def parseQuery(s: String): (Int, String) = {
import scala.util.{Failure, Success, Try}
val params = s.split(" ")
if (params.length != 2) (0, "")
else {
val n = Try(params(0).toInt) match {
case Success(n) => n
case Failure(_) => 0
}
val regex = "^\\[[<>]*\\]$".r
val path = if (regex.matches(params(1))) params(1).substring(1, params(1).length-1)
else ""
(n, path)
}
}
- the query is first split using blank as the separator
- the conversion of the first token to Int is then attempted using functional construct Try instead of imperative exception handling.
- if the path expression is correct, the enclosing square brackets are removed. This is achieved using params(1).substring(1, params(1).length-1) which omits the first and last character.
Processing the input
def main(args: Array[String]): Unit = {
val rule = Rule(readInt.toChar)
BTree(readLine()) match {
case Some(t) =>
val nrQueries = readInt()
assert(nrQueries > 0)
processInput(nrQueries, rule, Hist(t))
case None => System.exit(-1)
}
}
Method main() is very simple. First, it reads the rule and saves it as a Char. Then, it reads the serialised tree and tries to build a BTree based on it. The test cases run by hackerrank are guaranteed to be syntactically correct. So, we do not have to worry about invalid tree expressions.
After that, the number of queries is read. The core of the algorithm is implemented in method def processInput(nQueries: Int, rule: Rule, acc: Hist): Unit
@tailrec
def processInput(nQueries: Int, rule: Rule, acc: Hist): Unit = if (nQueries > 0) {
val (offset, path) = parseQuery(readLine())
val h = perform(offset, rule, acc)
println(h.hist(h.ix).readNode(path.toList).toString())
processInput(nQueries - 1, rule, h)
}
This method runs nQueries times and every time reads a query from the command line, processes it, and prints the result to the standard output.
Remark
In imperative languages, instead of writing tail-recursive method processInput() one would have written a simple loop (for or while) using modifiable data structures. The beauty of functional programming is that we can write equivalent code to the imperative which is equally efficient (being @tailrec) without dangerous side effects thanks to the use of immutable data.
Before looking into the perform() method we need to see how the history is implemented and how it works.
The history class
case class Hist(ix: Int, hist: Vector[BTree])
object Hist {
def apply(t: BTree): Hist = Hist(0, Vector(t))
}
We have seen above how the generations of transformed trees are persisted. This data structure contains all the transformations up to the previous generation, along with the position in the history. This is necessary because queries may require us to go back to the past (but not beyond generation 0)
Please note the convenience method apply() which, given a BTree, builds a history object initialised with this tree and an index at position 0.
Method perform()
def perform(offset: Int, rule: Rule, h: Hist): Hist = {
assert(h.hist.nonEmpty)
@tailrec
def run(times: Int, acc: Vector[BTree] = Vector.empty[BTree]): Vector[BTree] =
if (times < 1) acc
else run(times - 1, acc :+ acc.last.applyRule(rule))
val newIx = h.ix + offset
if (newIx < 0) h
else if (newIx < h.hist.length) Hist(newIx, h.hist)
else Hist(newIx, run(offset - (h.hist.length - h.ix - 1), h.hist))
}
- If the offset requires us to move to a position beyond the end of the existing history, method perform will apply the rule to the latest tree as many times as is required to fill the gap in the history.
- If instead the offset falls within the history, the entire history is returned, along with the new position determined by adding the offset to the previous position.
The updated history returned by method perform() allows method processInput() to print the result to the standard output using this simple statement: println(h.hist(h.ix).readNode(path.toList).toString())
This completes the explanation of the implementation. I hope you have enjoyed this article and have learned something useful. If you have found mistakes you can let me know using the contact form. Please consider that this article and the source code are provided as is. I write this content to the best of my knowledge but there is no guarantee that it is correct or otherwise suitable for any purpose.
Code of conduct
This content aims at making you a better programmer, but you may not use it to gain undeserved credits in programming challenges on any web site. If you want to take programming challenges, please write your own code and do not copy and paste this code because it is against the code of conduct.
Ok, enough with burocracy
If you came this far with this article you deserve a little treat. Here is my code on github:
https://github.com/maumorelli/alaraph
Thank you for reading and up Scala!!!
♦